Here is the paper link and its github repository:
Paper: MACE: Mass Concept Erasure in Diffusion Models
Shilin-LU/MACE[CVPR 2024] “MACE: Mass Concept Erasure in Diffusion Models” (Official Implementation)
Python36624
Preliminaries#
Latent Diffusion Models#
A Latent Diffusion Model (LDM) is comprised of two principle component: a vector quantization autoencoder and a diffusion model. The autoencoder undergoes pretrianing to transform images into spatial latent codes via an encoder \(z=\mathcal{E}(\mathbf{x})\), and it can recosntruct the images from these latent coes using a decoder \(\mathbf{x}\approx \mathcal{D}(\mathcal{E}(\mathbf{x}))\). The diffusion model is trained to geenrate latent codes that exist within the autoencoder’s latent space.
The training objective for the diffusion mdoel is defined as:
$$ \mathcal{L}_{\text{LDM}} = \mathbb{E} _{z\sim \mathcal{E}(\mathbf{x}), \mathbf{c}, \epsilon\sim\mathcal{N}(0, 1)} \left[||\epsilon-\epsilon _\theta(z_t, t, \mathbf{c})||^2_2\right] $$
where \(z_t\) is the noisy latent, \(t\) is the timestep, \(\epsilon\) is a standard Gaussian noise sample, \(\epsilon_\theta\) is the denoising network, and \(\mathbf{c}\) is the conditioning embeddings.
During the inference process, Gaussian noise is sampled as a starting point \(z_T\) and successively denoised to produce a new latent code \(z_0\) through the well-trained denoising network \(\epsilon_\theta\).
Ultimately, the latent code is transformed into an image via the pretrained decoder \(x_0\approx \mathcal{D}(z_0)\).
For more details of Diffusion models and Latent Diffusion Models, please refer to a very well-written blog Lil’Log.
Cross-attention in T2I diffusion models#
The cross-attention mechanism serve as the pivotal interface for the interplay between image and text modalities. Initially, a text prompt undergoes tokenization, coverting it into a series of unique token embeddings. These embeddings are then processed by a text encoder, such as CLIP 1, resulting in a final set of embeddings, wherein each token’s embedding \(e_i\) is enriched with information from the entire token sequence.
The embeddings are subsequently introduced into the cross-attention modules, where they act as navigational beacons for the image synthesis process. At certain layer \(l\) and timestep \(t\), the text embeddings are mapped using projection matrices, \(W_k\) and \(W_v\) to obtain the Keys \(k_{t,l}\) and Values \(v_{t,l}\). Concurrently, the image’s features \(f_{t,l}\) undergo the projection \(W_q\) to form the Queries \(q_{t,l}\). The cross-attention mechanism computes the attention map as:
$$ A_{t,l}=\text{softmax}(\frac{q_{t,l}\cdot k^\top_{t,l}}{\sqrt{d}}) $$
where \(d\) is the scaling factor to normalise the dot product. The module then synthesizes image features by aggregating Values with the attention weights \(o_{t,l}=A_{t,l}\cdot v_{t,l}\). This process ensures that the generated images are intricately aligned with the input text, completing the text-to-image generation with high fidelity.
For more details, please refer to detailed explained blog.
Closed-Form Cross-Attention Refinement#
Lu et al. 2 suggest a closed-form cross-attention refinement to encourage the model to refrain from embedding residual information of the target phrase into other words. They looked into the cross-attention layer, where the text embedding of a token encapsulates information from other tokens. This results in its Key and Value vectors.
In machine unlearning, a standard way of forgetting a concept is to find an anchor concept and make the target concept move to the anchor. In MACE, when altering the projection matrix \(W_k\), they modify it such that the Keys of the words that coexist with the target phrase in the prompt are mapped to the Keys of those same words in another prompt, where the target phrase is replaced with either its super-category or a generic concept. The illustration here is to show how closed-form cross-attention refinement can help remove residual.
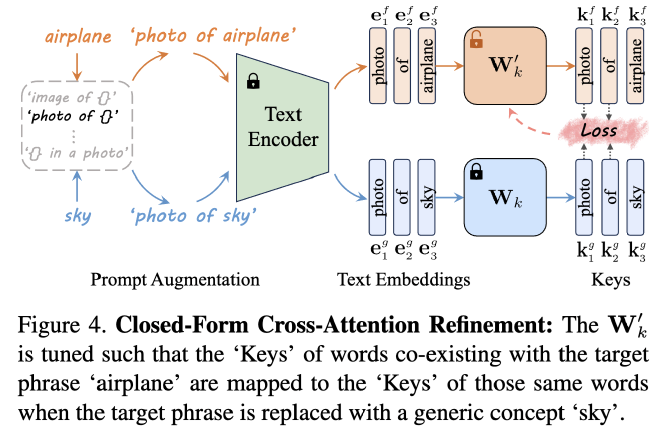
They fomulated the objective function as follows:
$$ \underset{W_{k}^{’}}{\min}\sum _{i=1}^{n}||W_k^{’}\cdot e_i^{f}-W_k^{’}\cdot e_i^{g}||^2_2+\lambda_1\sum _{i=n+1}^{n+m}| W_k^{’} \ \cdot e_i^{p} -W_k^{’}\cdot e_i^{p} | _2^{2} $$
where \(W_k^’\) is the pretrained weights, \(\lambda_1 \in \mathbb{R}^+\) is a hyperparameter, \(e_i^f\) is the embedding of a word co-existing with the target phrase, \(e^g\) is the embedding of that word when the target phrase is replaced with its super-category or a generic one, \(e^p\) is the embedding for preserving the prior, \(n, m\) are the number of embeddings for mapping and preserving. We can simply them as:
- \(e^f\): target concept embeddings.
- \(e^g\): anchor concept embeddings.
- \(e^p\): preservation embeddings.
The goal is to get a refined matrix, denoted as \(W^’_k \in \mathbb{R}^{d_1\times d_2}\), which encourages the model to refrain from embedding residual information, while preserving prior knowledge. To seek the optimal \(W^’_k\), we take the differentiation of the loss function and set the derivative equal to 0, that is:
$$ \begin{aligned} \frac{\partial \mathcal{L}(W’_k)}{\partial W’_k}&=2\sum _{i=1}^n \left(W’_k \cdot e^f_i (e^f_i)^\top - W_k\cdot e^g_i (e^f_i)^\top\right) \\ &+ 2 \lambda_1 \sum _{i=n+1}^{n+m} \left(W’_k\cdot e^p_i (e^p_i)^\top -W_k \cdot e^p_i(e^p_i)^\top\right) = 0 \end{aligned} $$
$$ \begin{aligned} \sum _{i=1}^n W’_k \cdot e^f_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} W’_k\cdot e^p_i (e^p_i)^\top &= \sum _{i=1}^n W_k \cdot e^g_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} W_k\cdot e^p_i (e^p_i)^\top \\ W’_k \left(\sum _{i=1}^n e^f_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} e^p_i (e^p_i)^\top\right) &= \sum _{i=1}^n W_k \cdot e^g_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} W_k\cdot e^p_i (e^p_i)^\top \\ \end{aligned} $$
$$ \begin{aligned} W’_k &= \left(\sum _{i=1}^n W_k \cdot e^g_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} W_k\cdot e^p_i (e^p_i)^\top\right)\cdot \left(\sum _{i=1}^n e^f_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} e^p_i (e^p_i)^\top\right)^{-1} \end{aligned} $$
One big issue it to ensure the second term right-hand side invertible, which is full rank. The author exaime the following quadratic form for any non-zero vector \(\mathbf{x}\in\mathbb{R}^{d_2}\) that:
$$ \begin{aligned} \mathbf{x}^\top\cdot \left(\sum _{i=1}^n e^f_i (e^f_i)^\top + \lambda_1 \sum _{i=n+1}^{n+m} e^p_i (e^p_i)^\top\right) \mathbf{x} &= \sum _{i=1}^n || \mathbf{x}^T e^f_i ||^2_2 + \lambda_1 \sum _{i=n+1}^{n+m} ||x^\top e^p_i||^2_2 \geq 0 \end{aligned} $$
In the paper, the authour utilised the MS-COCO dataset 3 that has more than 60 thousand captions for prior preserving, thus makes it highly improbable for all terms \(||x^\top e^p_i||^2_2\) in the sum to equal zero. Hence in general case, the matrix is positive definite and thus invertible.
Related Code#
Caching COCO#
Let’s get more details to look into the code. In MACE, the author first cache the coco captions as the preservation embeddings.
1train_annotation_file = './coco2014/annotations/captions_train2014.json'
2val_annotation_file = './coco2014/annotations/captions_val2014.json'
3
4# extract_prompts: a function that extract ['caption'] from ['annotations']
5train_prompts = extract_prompts(train_annotation_file)
6val_prompts = extract_prompts(val_annotation_file)
7# merge two prompt lists together
8total_prompts = train_prompts + val_prompts
After getting all MS-COCO captions, we first need to get all the related to_k and to_v layers that works on the interplay between text embedding and image features. Now we need to utilise the diffusers.StableDiffusionPipeline class to get the unet from Stable Diffusion v1.4 (we take this version for example). There is a very detailed explain of the architecture of Stable Diffusion Unet from labml.ai.
1model = "CompVis/stable-diffusion-v1-4"
2final_pipe = StableDiffusionPipeline.from_pretrained(model, torch_dtype=torch.float32).to("cuda")
3final_projection_matrices, final_ca_layers, final_og_matrices = get_ca_layers(final_pipe.unet, with_to_k=True)
Let’s take a closer look at how to extract each to_k and to_v layers from attn2 modules in the unet using get_ca_layers.
1def get_ca_layers(unet, with_to_k=True):
2 # go through the whole network
3 sub_nets = unet.named_children()
4 ca_layers = []
5 for net in sub_nets:
6 # check the up layers and down layers first
7 if 'up' in net[0] or 'down' in net[0]:
8 for block in net[1]:
9 # find the cross attention module
10 if 'Cross' in block.__class__.__name__ :
11 for attn in block.attentions:
12 for transformer in attn.transformer_blocks:
13 # we only need `attn2` as it is used for text embeddings and image features
14 ca_layers.append(transformer.attn2)
15 if 'mid' in net[0]:
16 for attn in net[1].attentions:
17 for transformer in attn.transformer_blocks:
18 # same as the `mid` layers
19 ca_layers.append(transformer.attn2)
20
21 ## get the value and key modules
22 # directly get the module, i.e., the Linear() layer
23 projection_matrices = [l.to_v for l in ca_layers]
24 # make a copy in case it gets overwritten
25 og_matrices = [copy.deepcopy(l.to_v) for l in ca_layers]
26 if with_to_k:
27 # the same for `to_k`
28 projection_matrices = projection_matrices + [l.to_k for l in ca_layers]
29 og_matrices = og_matrices + [copy.deepcopy(l.to_k) for l in ca_layers]
30
31 return projection_matrices, ca_layers, og_matrices
After we get the to_k and to_v modules (to calculate weights), all ca layers and the copy of to_k and to_v modules, we can define an empty cache_dict to store the embeddings, i.e., \(e^p_i\).
1cache_dict = {}
2for layer_num in tqdm(range(len(final_projection_matrices))):
3 cache_dict[f'{layer_num}_for_mat1'] = None
4 cache_dict[f'{layer_num}_for_mat2'] = None
5
6# process 500 items at a time
7step = 500
8for i in range(0, len(total_prompts), step):
9 entry = {"old": total_prompts[i:i+step], "new": total_prompts[i:i+step]}
10
11 contexts, valuess = prepare_k_v(final_pipe.text_encoder,
12 final_projection_matrices,
13 final_ca_layers,
14 final_og_matrices,
15 [entry],
16 final_pipe.tokenizer,
17 all_words=True)
18
19 closed_form_refinement(final_projection_matrices,
20 contexts, valuess,
21 cache_dict=cache_dict, cache_mode=True)
22 # delete cache to save GPU memory
23 gc.collect()
24 torch.cuda.empty_cache()
25
26 print(f'==================== num: {i}/{len(total_prompts)}====================')
27 # save parted volumes in case
28 if i % 10000 == 0:
29 torch.save(cache_dict, f"./cache/coco/cache_{i}.pt")
30
31torch.save(cache_dict, f"./cache/coco/cache_final.pt")
In the code above there are two very important functions we need to take care: prepare_k_v and closed_form_refinement.
Prepare to_k and to_v#
Let’s first look at prepare_k_v function. Since the texts_old and texts_new are identity in caching MS-COCO case (purpose for preservation), \(e^f\) and \(e^g\) in the following comments are both refer to \(e^p\).
1def prepare_k_v(text_encoder,
2 projection_matrices,
3 ca_layers,
4 og_matrices,
5 test_set,
6 tokenizer,
7 with_to_k=True,
8 all_words=False,
9 prepare_k_v_for_lora=False):
10
11 """
12 text_encoder: the text encoder from Stable Diffusion Pipeline
13 projection_matrices: the temperory `to_k` and `to_v` modules
14 ca_layers: the cross-attention layers
15 og_matrices: the copy of `to_k` and `to_v` modules
16 test_set: the prompts that needs to be processed, will be e^f and e^g later
17 tokenzier: the tokenizer from Stable Diffusion Pipeline
18 with_to_k: whether modify `to_k` weights
19 all_words:
20 prepare_k_v_for_lora: for later lora training
21 """
22
23 with torch.no_grad():
24 # initialise full e^f and e^g list
25 all_contexts, all_valuess = [], []
26
27 for curr_item in test_set:
28 gc.collect()
29 torch.cuda.empty_cache()
30
31 #### reinitialise LDM parameters using the backup copy
32 num_ca_clip_layers = len(ca_layers)
33 for idx_, l in enumerate(ca_layers):
34 l.to_v = copy.deepcopy(og_matrices[idx_])
35 projection_matrices[idx_] = l.to_v
36 if with_to_k:
37 l.to_k = copy.deepcopy(og_matrices[num_ca_clip_layers + idx_])
38 projection_matrices[num_ca_clip_layers + idx_] = l.to_k
39
40 old_embs, new_embs = [], []
41 extended_old_indices, extended_new_indices = [], []
42
43 #### indetify corresponding destinations for each token in old_emb
44 # Bulk tokenization
45 texts_old = [item[0] for item in curr_item["old"]]
46 texts_new = [item[0] for item in curr_item["new"]]
47 # concat two lists together to get tokenized
48 texts_combined = texts_old + texts_new
49
50 tokenized_inputs = tokenizer(
51 texts_combined,
52 padding="max_length",
53 max_length=tokenizer.model_max_length,
54 truncation=True,
55 return_tensors="pt"
56 )
57
58 # using tokens to get text embeddings
59 text_embeddings = text_encoder(tokenized_inputs.input_ids.to(text_encoder.device))[0]
60 # seperate old_embeds and new_embeds
61 old_embs.extend(text_embeddings[:len(texts_old)])
62 new_embs.extend(text_embeddings[len(texts_old):])
63
64 # Find matching indices
65 for old_text, new_text in zip(texts_old, texts_new):
66 tokens_a = tokenizer(old_text).input_ids
67 tokens_b = tokenizer(new_text).input_ids
68
69 # find_mathing_indices function is to find two sequence indecies of
70 # their common and different part
71 old_indices, new_indices = find_matching_indices(tokens_a, tokens_b)
72 # If found difference, needs to padding to the same length
73 if old_indices[-1] >= new_indices[-1]:
74 extended_old_indices.append(old_indices + list(range(old_indices[-1] + 1, 77)))
75 extended_new_indices.append(new_indices + list(range(new_indices[-1] + 1, 77 - (old_indices[-1] - new_indices[-1]))))
76 else:
77 extended_new_indices.append(new_indices + list(range(new_indices[-1] + 1, 77)))
78 extended_old_indices.append(old_indices + list(range(old_indices[-1] + 1, 77 - (new_indices[-1] - old_indices[-1]))))
79
80 #### prepare batch: for each pair of setences, old context and new values
81 contexts, valuess = [], []
82 if not all_words:
83 # only use the differences part to save time and memory
84 for idx, (old_emb, new_emb) in enumerate(zip(old_embs, new_embs)):
85 # get the e^f embedding
86 context = old_emb[extended_old_indices[idx]].detach()
87 values = []
88 for layer in projection_matrices:
89 # get the W_k * e^g embedding, !!note W_k is introduced here!!
90 values.append(layer(new_emb[extended_new_indices[idx]]).detach())
91 contexts.append(context)
92 valuess.append(values)
93
94 all_contexts.append(contexts)
95 all_valuess.append(valuess)
96 else:
97 if prepare_k_v_for_lora:
98 # prepare for lora, then no need to use new_emb
99 for idx, old_emb in enumerate(old_embs):
100 context = old_emb.detach()
101 values = []
102 for layer in projection_matrices:
103 values.append(layer(old_emb).detach())
104 contexts.append(context)
105 valuess.append(values)
106 else:
107 # need to use new_emb, both common and difference part
108 for idx, (old_emb, new_emb) in enumerate(zip(old_embs, new_embs)):
109 context = old_emb.detach()
110 values = []
111 for layer in projection_matrices:
112 values.append(layer(new_emb).detach())
113 contexts.append(context)
114 valuess.append(values)
115
116 all_contexts.append(contexts)
117 all_valuess.append(valuess)
118
119 # return e^f and e^g lists
120 return all_contexts, all_valuess
Closed-form Solution#
Now we got e^p for caching coco, we can use the derived formula above to get the closed-form solution by using the function closed_form_refinement.
1def closed_form_refinement(projection_matrices,
2 all_contexts=None,
3 all_valuess=None,
4 lamb=0.5,
5 preserve_scale=1,
6 cache_dict=None,
7 cache_dict_path=None,
8 cache_mode=False):
9 """
10 projection_matrices: the `to_k` and `to_v` modules,
11 all_contexts: the e^f or e^p embeddings
12 all_valuess: the e^g or e^p embeddings
13 lamb: the hyperparameter weight of the initialisation
14 preserve_scale: the hyperparameter weight of the preservation,
15 cache_dict: the calculated weights dict
16 cache_dict_path: should read pre-cached weight dict or not
17 cache_mode: should cache or not
18 """
19
20 with torch.no_grad():
21 if cache_dict_path is not None:
22 cache_dict = torch.load(cache_dict_path, map_location=projection_matrices[0].weight.device)
23
24 for layer_num in tqdm(range(len(projection_matrices))):
25 gc.collect()
26 torch.cuda.empty_cache()
27
28 # the first term of the closed-formed solution, initlised with the original weights
29 mat1 = lamb * projection_matrices[layer_num].weight
30 # the second term of the closed-form solution, the inversed term
31 mat2 = lamb * torch.eye(projection_matrices[layer_num].weight.shape[1], device=projection_matrices[layer_num].weight.device)
32
33 # the container for first term and second term
34 total_for_mat1 = torch.zeros_like(projection_matrices[layer_num].weight)
35 total_for_mat2 = torch.zeros_like(mat2)
36
37 if all_contexts is not None and all_valuess is not None:
38 for contexts, valuess in zip(all_contexts, all_valuess):
39 # Convert contexts and values to tensors
40 contexts_tensor = torch.stack(contexts, dim=2)
41 values_tensor = torch.stack([vals[layer_num] for vals in valuess], dim=2)
42
43 # Aggregate sums for mat1, mat2 using matrix multiplication
44 # calculate e^g \cdot e^f^top
45 for_mat1 = torch.bmm(values_tensor, contexts_tensor.permute(0, 2, 1)).sum(dim=0)
46 # calculate e^f \cdot e^f^top
47 for_mat2 = torch.bmm(contexts_tensor, contexts_tensor.permute(0, 2, 1)).sum(dim=0)
48
49 # sum for each term
50 total_for_mat1 += for_mat1
51 total_for_mat2 += for_mat2
52
53 del for_mat1, for_mat2
54
55 # if store the weights
56 if cache_mode:
57 # cache the results to save memory only
58 # coco goes here
59 if cache_dict[f'{layer_num}_for_mat1'] is None:
60 cache_dict[f'{layer_num}_for_mat1'] = total_for_mat1
61 cache_dict[f'{layer_num}_for_mat2'] = total_for_mat2
62 else:
63 cache_dict[f'{layer_num}_for_mat1'] += total_for_mat1
64 cache_dict[f'{layer_num}_for_mat2'] += total_for_mat2
65 else:
66 # CFR calculation
67 # add the preservation term e^p \cdot e^p^\top
68 if cache_dict_path is not None or cache_dict is not None:
69 total_for_mat1 += preserve_scale * cache_dict[f'{layer_num}_for_mat1']
70 total_for_mat2 += preserve_scale * cache_dict[f'{layer_num}_for_mat2']
71
72 total_for_mat1 += mat1
73 total_for_mat2 += mat2
74
75 # get the final calculation
76 projection_matrices[layer_num].weight.data = total_for_mat1 @ torch.inverse(total_for_mat2)
77
78 del total_for_mat1, total_for_mat2
For simplicity, take closed_form_refinement(final_projection_matrices, contexts, valuess, cache_dict=cache_dict, cache_mode=True) for example. Since we already got final_projection_matrices, which is the to_k and to_v modules of the cross-attention layers, contexts and valuess are the caption embeddings for coco, the cache_dict is empty at first, and cache_mode is set to True here. At first, it initialise the two terms to the weight of final_projection_matrices and an identity matrix, and then calculate \(e^p \cdot (e^p)^{\top}\) for both terms. Since it is in cache_mode, we only save the first term and second term, i.e. \(W’_k \lambda_1 \sum _{i=n+1}^{n+m} e^p_i (e^p_i)^\top\) and \(\lambda_1 \sum _{i=n+1}^{n+m} e^p_i (e^p_i)^\top\) for later use. For unlearning part, when set cache_mode to False, it will get in the else branch, adding preservation term from cache_dict and multiplying the inverse as the formula.
In addition to retaining general prior knowledge, the MACE framework extends support to allow users to highlight the preserve domain-specific concepts. The only difference is to add another term of \(W’_k \lambda_3 \sum _{i=n+m’}^{n+m} e^p_i (e^p_i)^\top\) and \(\lambda_3 \sum _{i=n+m’}^{n+m} e^p_i (e^p_i)^\top\), where \(m’\) is a number of terms of general knowledge and \(m-m’\) is a number of terms of domain-specific knowledge. This term is usually absent in most tasks, only useful in celebrity unlearning.
Radford, Alec, et al. “Learning transferable visual models from natural language supervision.” International conference on machine learning. PMLR, 2021. ↩︎
Lu, Shilin, et al. “Mace: Mass concept erasure in diffusion models.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2024. ↩︎
Lin, Tsung-Yi, et al. “Microsoft coco: Common objects in context.” Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part V 13. Springer International Publishing, 2014. ↩︎